BTC_POWER_LA
現在、コンテンツはありません
BTC_POWER_LA
Scientific Bitcoin Instituteのディレクターの外観。
原文表示
- 報酬
- いいね
- コメント
- リポスト
- 共有
人々はパワー・ロウの誤った解釈をしています。彼らはパワー・ロウの周りにバンドを考えています。これらは比較的大きなものであり、過去に示したように、ビットコインがほとんどの時間を費やす場所に焦点を当てるとそうではないことがわかります。
しかし、実際にはバンドの概念は、真のビットコインの挙動を理解する上で重要ではありません。本当の意味を理解するには、正規化リターンや日次傾斜の言語を使う必要があります。
1. 根本的な問題:生のリターンは誤解を招く
ビットコインの生の日次リターンや生の価格変動を見ると、すぐに二つの問題に直面します。
非定常性
2011年の5%の動きは、経済的意味、流動性、システム規模の点で2024年の5%の動きと比較できません。
ボラティリティは「減衰」しているように見えますが、この減衰は成長と絡み合っています。
スケール依存性
システムが成長するにつれて絶対価格変動が爆発的に増加します。
パーセンテージリターンでさえ、システムの自然な時間スケールが変化している事実を隠しています。
要するに:生のリターンは成長とノイズを混合しており、ビットコインを安定したシステムとして研究することを不可能にしています。
2. パワー・ロウを自然な正規化として
パワー・ロウは時間と成長の自然な正規化を提供します。
価格が次のように従う場合:
P(t) = C · t^α
このとき、期待され
しかし、実際にはバンドの概念は、真のビットコインの挙動を理解する上で重要ではありません。本当の意味を理解するには、正規化リターンや日次傾斜の言語を使う必要があります。
1. 根本的な問題:生のリターンは誤解を招く
ビットコインの生の日次リターンや生の価格変動を見ると、すぐに二つの問題に直面します。
非定常性
2011年の5%の動きは、経済的意味、流動性、システム規模の点で2024年の5%の動きと比較できません。
ボラティリティは「減衰」しているように見えますが、この減衰は成長と絡み合っています。
スケール依存性
システムが成長するにつれて絶対価格変動が爆発的に増加します。
パーセンテージリターンでさえ、システムの自然な時間スケールが変化している事実を隠しています。
要するに:生のリターンは成長とノイズを混合しており、ビットコインを安定したシステムとして研究することを不可能にしています。
2. パワー・ロウを自然な正規化として
パワー・ロウは時間と成長の自然な正規化を提供します。
価格が次のように従う場合:
P(t) = C · t^α
このとき、期待され
BTC-1.48%
- 報酬
- いいね
- コメント
- リポスト
- 共有
私の孫は立派なイタリア人として成長しています。
原文表示
- 報酬
- いいね
- コメント
- リポスト
- 共有
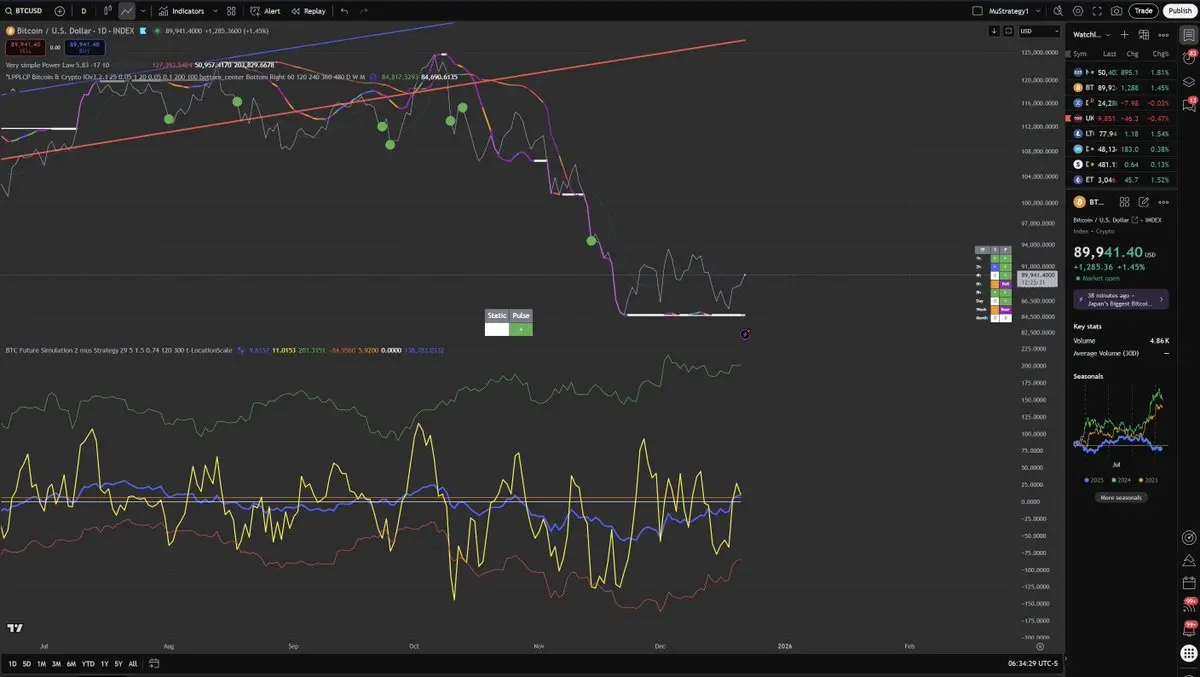
下のパネルの青い線は、2週間のウィンドウで計算された平均パワーロー傾斜を表しています。現在、長期的な値である5.9を超えており、これは全体の回帰から得られたのと同じ指数です。
これは、パワー・ローのトレンド自体がその平均に戻りつつあることを示しています。価格はまだ回帰線に戻ってはいませんが、成長レジームの方向性が回復しています。
言い換えれば、価格が一時的にパワー・ロー成長パスから押し出されるたびに、その偏差は歴史的に一時的なものでした。システムは時間の経過とともに、基礎となるパワー・ローのトレンドに一貫して再調整されます。
原文表示これは、パワー・ローのトレンド自体がその平均に戻りつつあることを示しています。価格はまだ回帰線に戻ってはいませんが、成長レジームの方向性が回復しています。
言い換えれば、価格が一時的にパワー・ロー成長パスから押し出されるたびに、その偏差は歴史的に一時的なものでした。システムは時間の経過とともに、基礎となるパワー・ローのトレンドに一貫して再調整されます。
- 報酬
- いいね
- コメント
- リポスト
- 共有
ルガーノの起源に戻る。
原文表示
- 報酬
- いいね
- コメント
- リポスト
- 共有
今日はもう一人のタクシードライバーにオレンジピルをしましたが、さらに驚いたことに、鉄道警察官とビットコインについて話しながら彼女がパトロールをしている最中に話しました(彼女はすでにビットコイナーでした)。
私たちは残りの隊員と一緒にオレンジピルを終えました。
私たちは残りの隊員と一緒にオレンジピルを終えました。
BTC-1.48%
- 報酬
- いいね
- コメント
- リポスト
- 共有
ヴァリエッジョ。
原文表示
- 報酬
- いいね
- コメント
- リポスト
- 共有
- 報酬
- いいね
- コメント
- リポスト
- 共有
素晴らしいことが起こる。再びルガーノでイタリア・スイス大学や他の大学の教授たちと会い、ビットコインに関する学術的取り組みについて議論しました。
多くの素晴らしいアイデアや全体的なビジョンが、ビットコインは真剣な科学的研究に値する現象であることを支持しています。
続報をお待ちください。
多くの素晴らしいアイデアや全体的なビジョンが、ビットコインは真剣な科学的研究に値する現象であることを支持しています。
続報をお待ちください。
BTC-1.48%
- 報酬
- いいね
- コメント
- リポスト
- 共有
今すぐトリノ工科大学でのパワー法に関するライブ講義にご参加ください。リンクは下記です。
原文表示- 報酬
- いいね
- コメント
- リポスト
- 共有
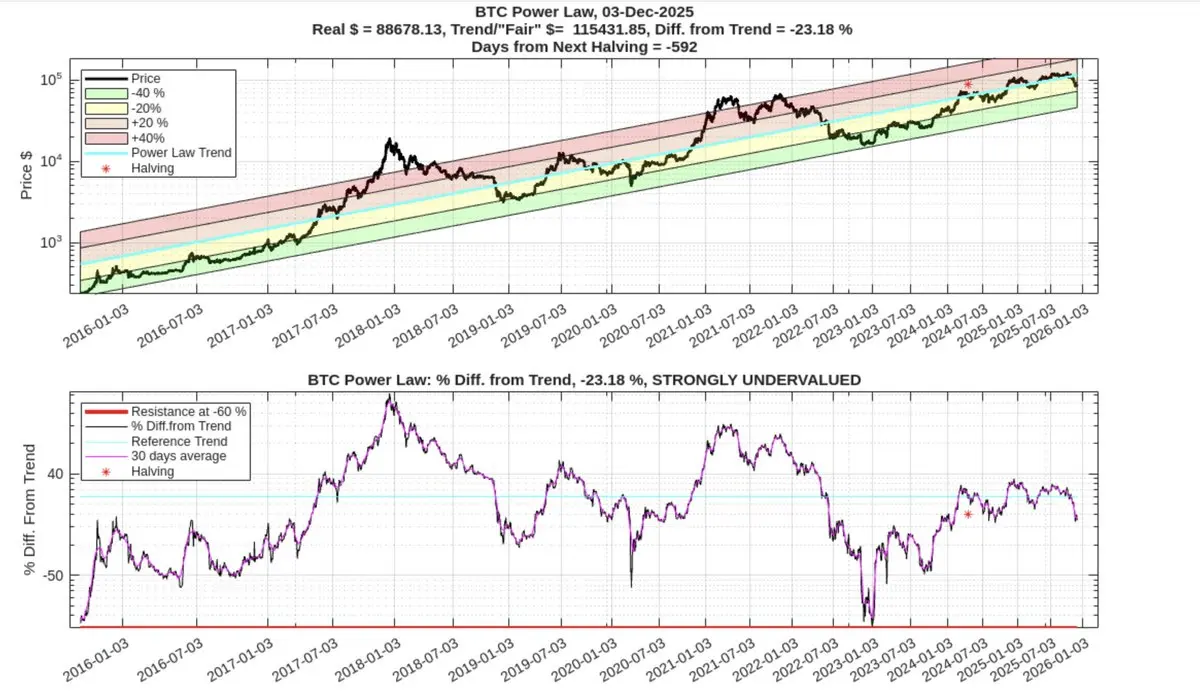
93Kで、パワーローから約19%の位置にいます。
ビットコインのボラティリティを考えると、これはかなり注目に値します。強気相場がなくても、長期的にはパワーローが予測する通りに成長し続けています。
ビットコインのボラティリティを考えると、これはかなり注目に値します。強気相場がなくても、長期的にはパワーローが予測する通りに成長し続けています。
BTC-1.48%
- 報酬
- いいね
- コメント
- リポスト
- 共有
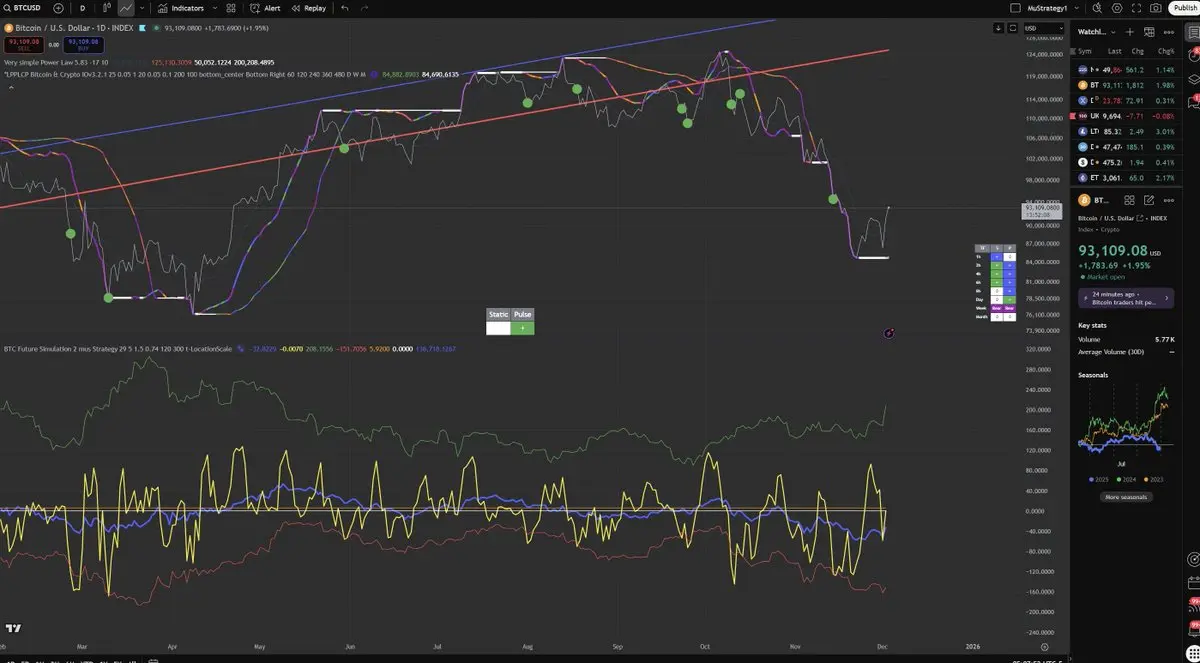
実際、ビットコインがこうした外科的な流動性スイープから回復する能力には感心しています。
パワーローの日次傾斜(下部パネル)は、16年間追い続けてきた平均値に戻りつつあります。
クリティカルパルス信号(上部パネル)は、状態変化が起きていることを示す白線を表示していますが、完全な状態変化を確認するには、2つの主要な信号が分離する必要があります。
パワーローの日次傾斜(下部パネル)は、16年間追い続けてきた平均値に戻りつつあります。
クリティカルパルス信号(上部パネル)は、状態変化が起きていることを示す白線を表示していますが、完全な状態変化を確認するには、2つの主要な信号が分離する必要があります。
BTC-1.48%
- 報酬
- いいね
- コメント
- リポスト
- 共有
ショーはここでも見ることができます:
原文表示- 報酬
- いいね
- コメント
- リポスト
- 共有
- 報酬
- いいね
- コメント
- リポスト
- 共有
中央ヨーロッパ時間の午後2時、または東部標準時間の午前8時に、クリスとジョバンニとの "ビットコイン・コンプレキシティ・パルス" を開催します。
複雑系科学のツールを使用して、現在の市場状況について議論します。
そのショーはX、YouTube、Twitchで行われます。
複雑系科学のツールを使用して、現在の市場状況について議論します。
そのショーはX、YouTube、Twitchで行われます。
BTC-1.48%

- 報酬
- いいね
- コメント
- リポスト
- 共有
- 報酬
- いいね
- コメント
- リポスト
- 共有