BTC_POWER_LA

我們將於太平洋標準時間晚上7:00舉行第38集《比特幣物理學》節目。
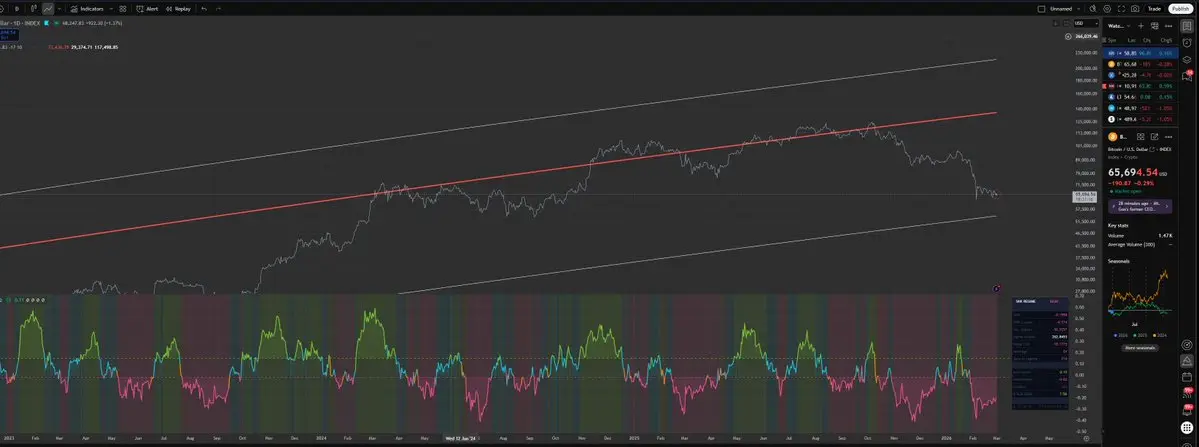
我將討論新的幾何法則指標：信噪比斜率。
我還將宣布我們的《比特幣物理學》書籍(已開始預購)。
Stephen的議程如下。
很快見！

早上醒來聞到綠色蠟燭的味道真是太好了。
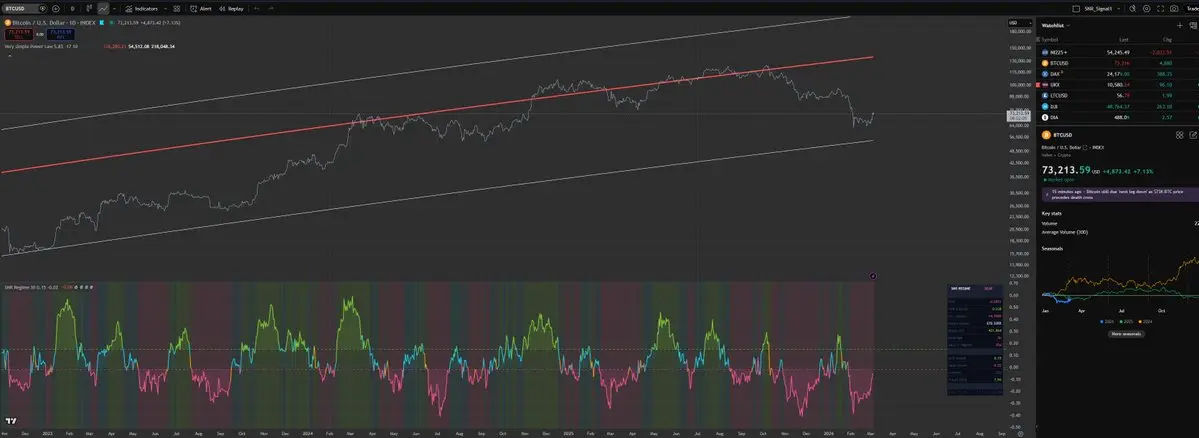
新的 Slope Signal 指標顯示我們正接近轉折點，從熊市轉向牛市。

今晚一切都好 (永不讓我失望) 看到星星，它們閃耀著光芒 (永不讓我失望)。

來自《比特幣的物理學》導言。
今天的比特幣對不同的人來說是多重身份的存在。
對投資者而言，它是一個擁有十六年非凡但波動性回報記錄的資產。對技術專家而言，它是第一個成功實現去中心化共識機制的方案——一個解決分布式計算中長期未解問題的方案。對自由意志主義者和公民自由倡導者而言，它是超越國家控制範圍的金融主權工具。
對經濟學家而言，它是一個實驗，觀察當你移除貨幣系統的制度支架後，剩下的價值會是什麼。對中央銀行家和金融監管者而言，它是一個對現有貨幣政策和金融監督框架的全新挑戰。
這些觀點都不錯。比特幣同時具備這些特性。
本書要探討的問題是另一個：它在其基本動力層面上，是什麼樣的存在？而證據——也是本書的論點——顯示的答案是：比特幣是一個複雜的物理系統：一個由自我組織的網絡，受與生物、城市和地震相同的數學定律支配。
將其理解為這樣的系統，會改變你能提出的問題、能做出的預測，以及你應該如何評估關於它的各種說法。

我告訴ChatGPT，Grok 修正了ChatGPT創建的圖片文字中的拼寫錯誤。
它用幽默的方式接受了，甚至還用了一個表情符號。看到這些AI具有個性，令人感到溫暖。

我喜歡這個。
這幅壁畫以比特幣和科學探索的視角，重新想像了經典的工業壁畫。在其中心，一個閃耀的比特幣球體懸浮在幾何環中，象徵著支配網絡的數學和熱力學定律。背後站著一位科學家，雙手張開，並非控制系統，而是在研究並與之協調。
左側，逐漸消退的法幣世界顯得混亂且熵增：印鈔機、債務機器和失序的市場。右側，一個去中心化的生態系統浮現，礦工、節點、程式設計師、家庭和點對點連接形成一個閃耀的合作網絡。
上方，螺旋星系和微弱的對數網格喚起尺度不變性和冪律；下方，根系將能量轉化為安全與繁榮。
這幅壁畫將比特幣呈現為一種科學和文明的演進，而非意識形態，根植於可測量的法則之中。

比特幣壁畫。

科學比特幣研究所的使命（以圖像呈現）。

TradingView 指標，提供讓我們從 1 BTC 賺取 800 BTC 的交易信號。